Current quantum computer research would be impossible without high-precision RF test & measurement equipment

Max Werninghaus, Walther-Meißner-Institute

To solve complex problems, quantum computers exploit natural quantum properties. As with conventional bits, logic states are represented and processed using quantum bits (qubit). Whereas a conventional bit is binary, a qubit can simultaneously exist in combinations of two states.

This phenomenon is known as superposition and cannot be explained using the laws of classical physics. Superposition is a purely quantum mechanical property and is the basis for the enormous computational potential of quantum computers.

Superconducting qubits

Research currently focuses on the technical implementation of qubits. One promising area is superconducting qubits that use electrical circuits to store electromagnetic fields with a very long half life thanks to their loss-free superconductivity. A resonant circuit is designed to effectively produce a controllable two-state system. The resonance frequency for this type of circuit is typically in the microwave range at 5 GHz. The base state of the resonant circuit is logic state zero, while the first excited state is logic state one.

Systematic control of these two states is still not possible without added structures. In harmonic oscillators, such as LC resonant circuits, the spacing between two adjacent energy states is always equal (harmonicity). One side effect is the uncontrolled shifting of a resonant microwave signal in a circuit either from the base state to the first excited state, or from an arbitrary excited state to the next higher state. Nonlinear inductances can cancel out harmonicity. Josephson junctions help create two distinct energy states that can be used as a controllable qubit. They give the transition from the base state to the first excited state a characteristic frequency that is unique to this transition. Because the property mimics atomic electron transitions, superconducting qubits are also known as artificial atoms.

A quantum state is extremely fragile. The operating temperature for a superconducting qubit is around 10 millikelvin or about –273 °C, which is very close to absolute zero. This is the only way to keep the thermal background noise

Controlling quantum states with microwave signals

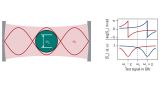
The energy state of a qubit can be controlled with external microwave signals. A Bloch sphere illustrates this process (Figure, right). The one and zero logic states are located at the north and south poles of the Bloch sphere. Every other point on the surface of the sphere corresponds to a superposition state. The current state is indicated by the so-called state vector. Interaction with a resonant microwave signal causes rotation of the state vector in the Bloch sphere.

To perform dependable computing operations with qubits, this rotation needs to be controlled with great precision based on the pulse length, microwave signal amplitude and the control pulse envelope. The so-called relative phase of the control pulse influences the rotation axis of the qubit state in the Bloch sphere. When pulses with the same phase are applied to the qubit, the state always rotates on e.g. the x-axis. If a pulse is phase-shifted by 90°, the state vector will rotate on the y-axis.

Signal source requirements

Arbitrary waveform generators are reliable, flexible control signal sources. Together with microwave sources and mixers, the right pulses can be generated at the right qubit frequency. By precisely regulating the control pulse phase in real time and exact control of the envelopes, any desired target point on a Bloch sphere can be reached at any time from any starting point.

Unlike conventional computing operations with a high error tolerance, quantum computers rely on precise calibration of control pulses. Even tiny deviations in the rotation (over rotation of the quantum state by 1 %) can alter the resulting quantum operation. Similar errors occur with inaccurate phase control. Control instruments for quantum computers must therefore have high phase and amplitude stability. Control pulse phases are regulated by the in-phase and quadrature components of the pulse stored on the arbitrary waveform generator.

Quantum algorithms and quantum computer experiments are complex. Both require output of a large number of signal pulses on multiple channels with relevant phase stability and timing synchronization. This often leads to long wait times during initialization of conventional control hardware and can ultimately limit the complexity of planned experiments. Various manufacturers of microwave generators have recently begun developing special instruments together with quantum computing scientists.

These instruments can do much more than conventional arbitrary waveform generators and satisfy some of the special research requirements in this field. Pulse phases can be managed directly on the instrument with field programmable gate arrays (FPGA), drastically reducing the required storage space. And even complex quantum algorithms that involve thousands of operations can be reduced to a manageable set of fundamental operations. There is no need to store a continuous signal in the arbitrary waveform generator for each quantum algorithm. A set of fundamental operations along with information about the output sequence are enough. Specialized arbitrary waveform generators for quantum computer research already support such functions.

Signal analysis for selecting quantum states

Once a quantum computer runs an operation, the quantum states of the qubits are selected and the qubits are coupled to readout resonators. Due to interaction with the qubit, the resonance frequency of the resonator is shifted depending on the qubit state (Figure). By stimulating it with a readout signal near the resonance frequency, it becomes possible to deduce the qubit state based on the shift in the signal’s amplitude and phase in transmission or reflection.

Current quantum technology advances allow effective operation of the relevant control electronics and quantum hardware. By directly integrating signal analysis functions into instruments, quantum algorithm results can be observed in real time. Intelligent arbitrary waveform generators simplify working with quantum computers in the same way that assemblers have long been used in computer and machine programming. One of the main challenges here is synchronizing and coordinating the hundreds of signals needed to operate larger quantum computers.