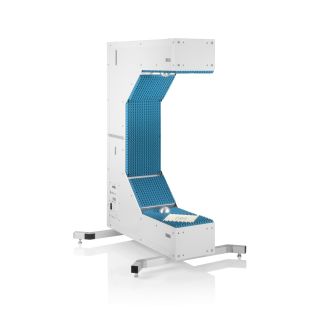
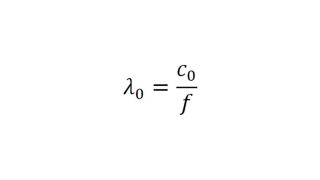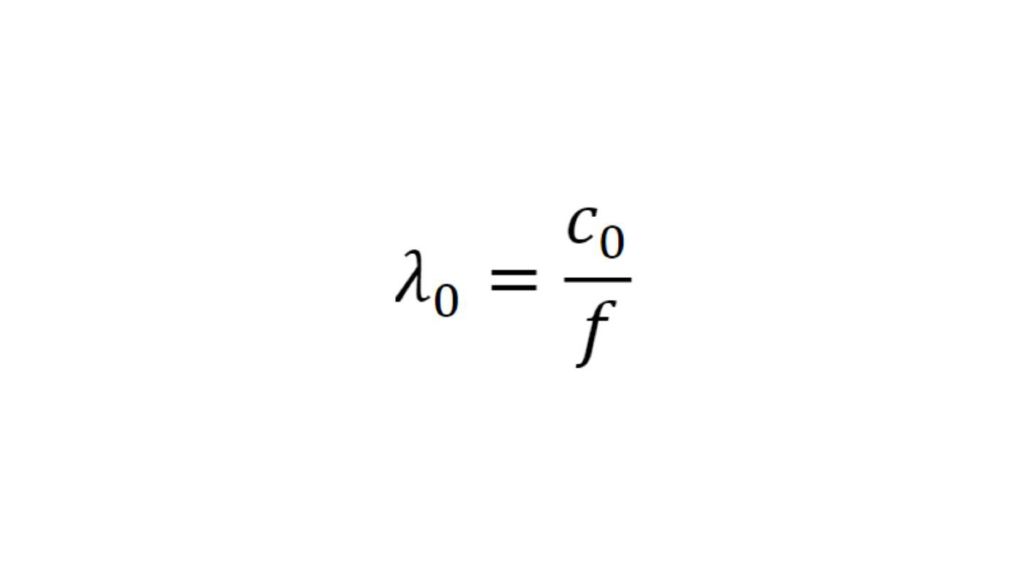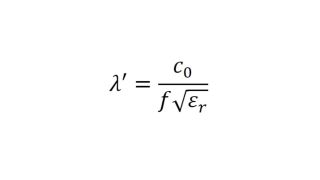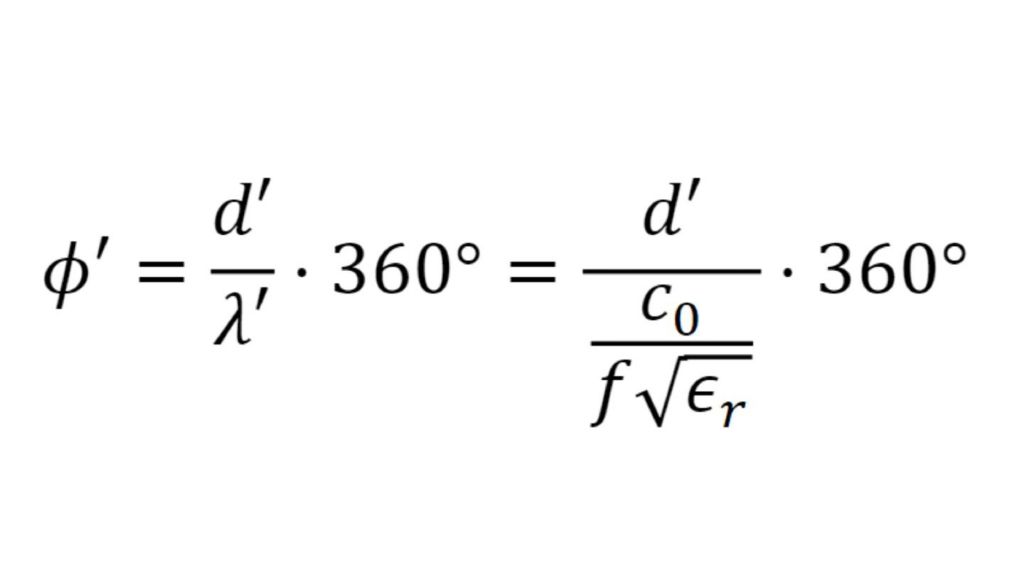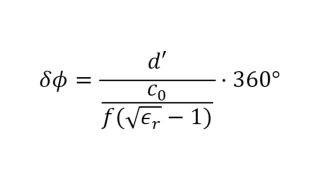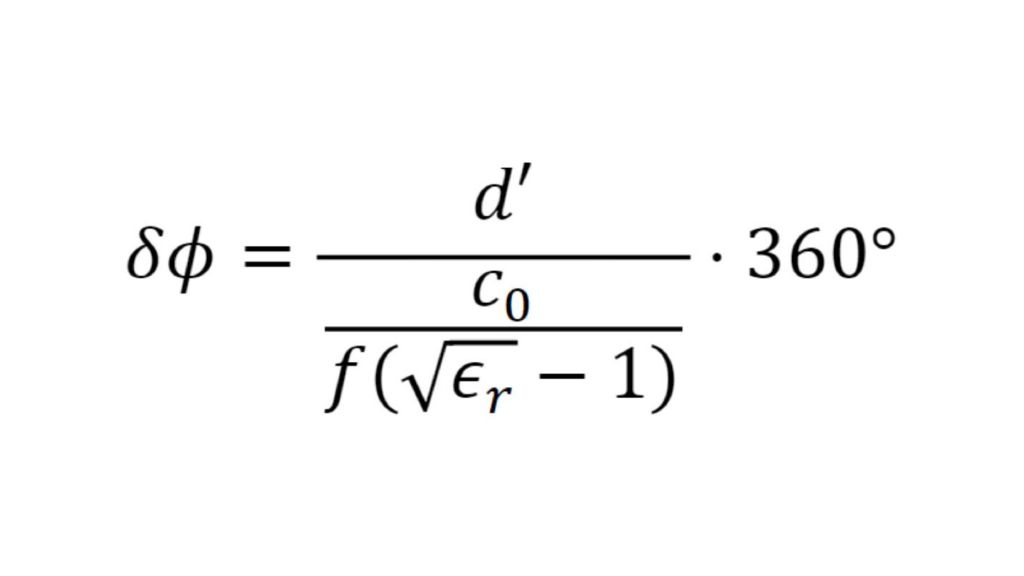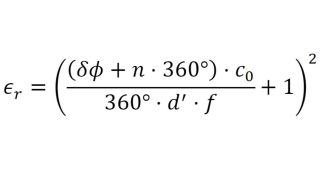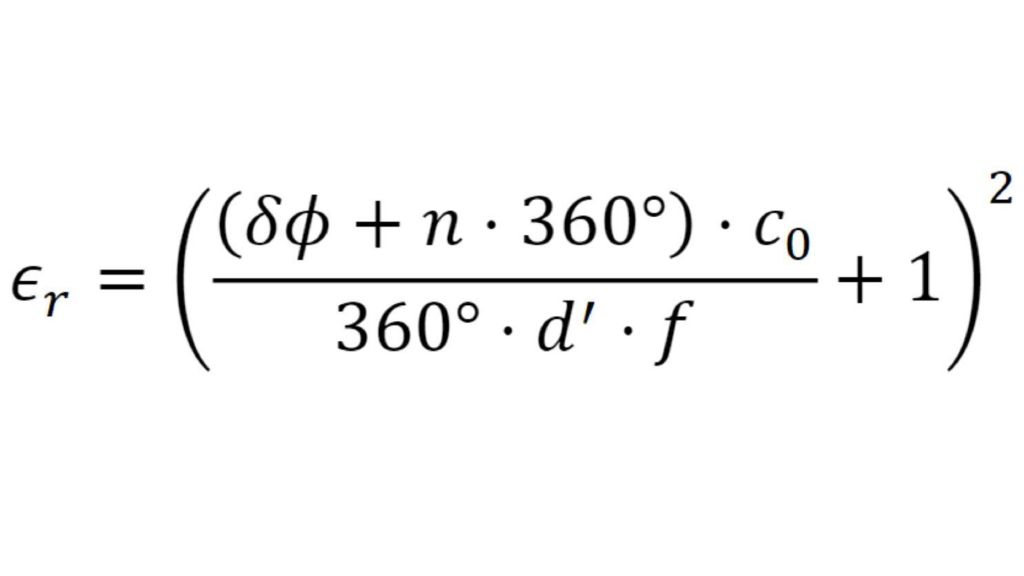Caracterizar las propiedades de materiales poliméricos para aplicaciones de automoción
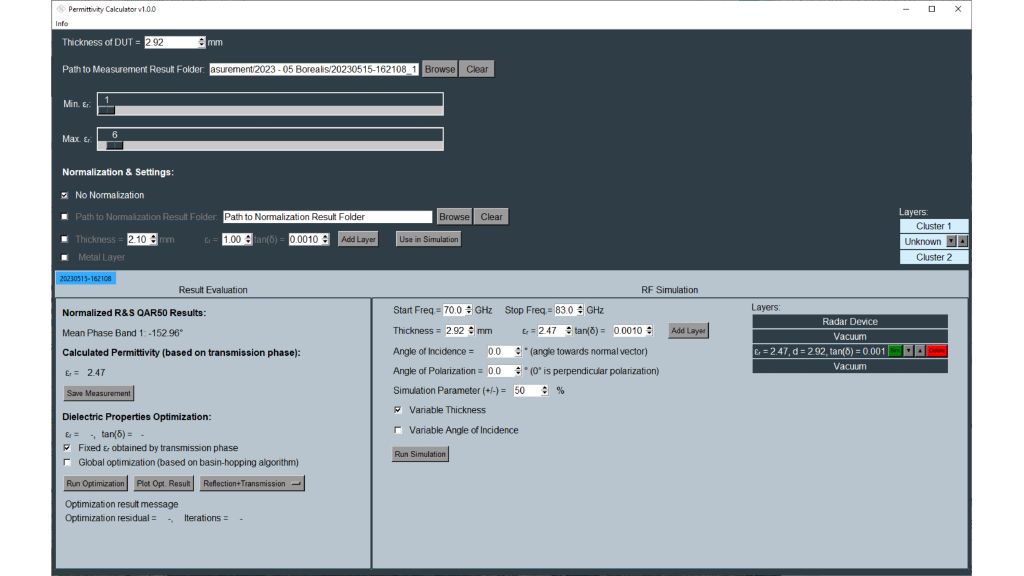
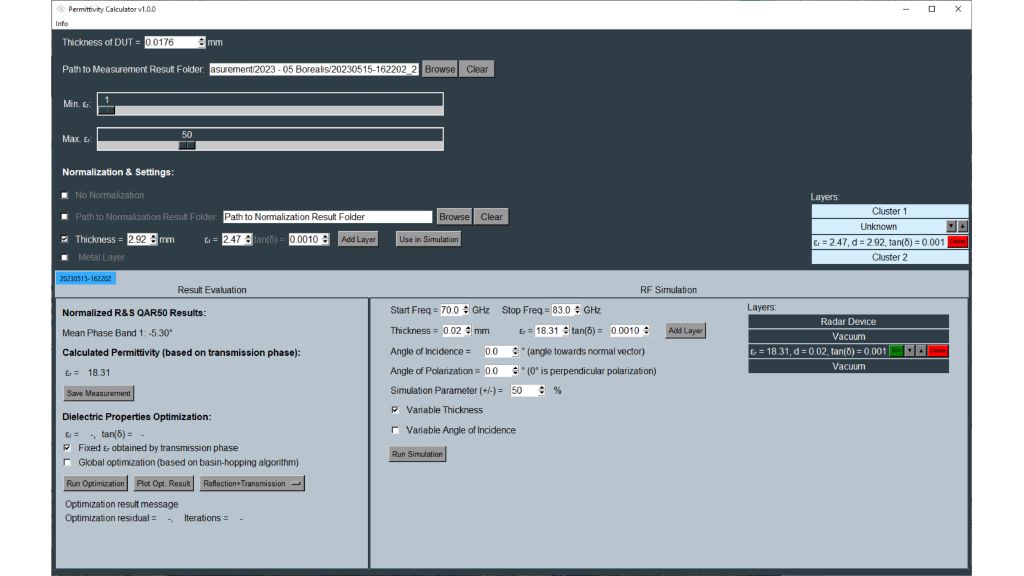
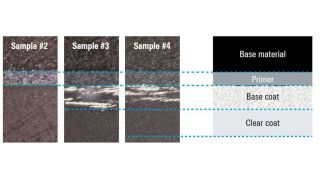
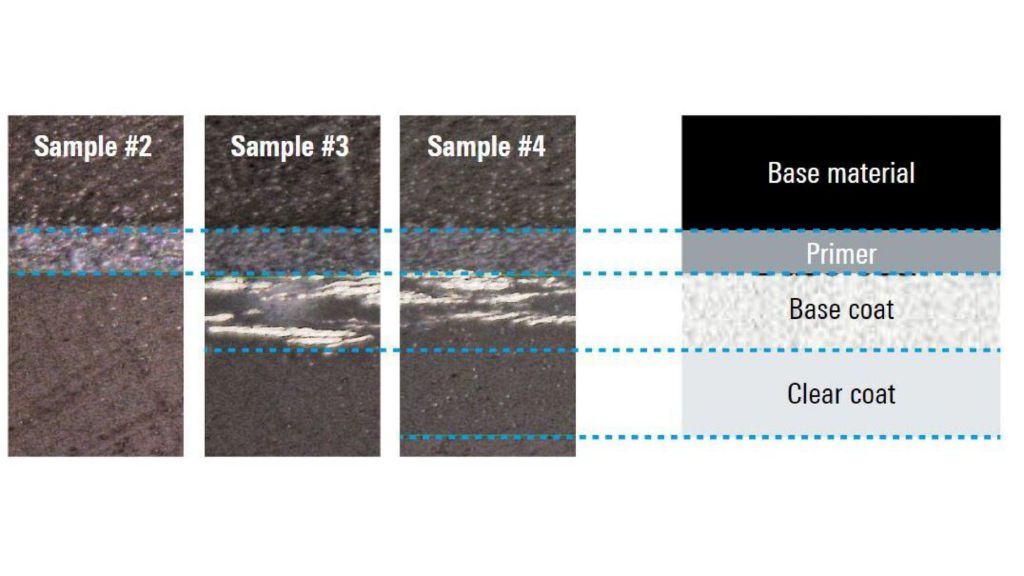
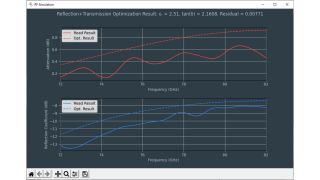
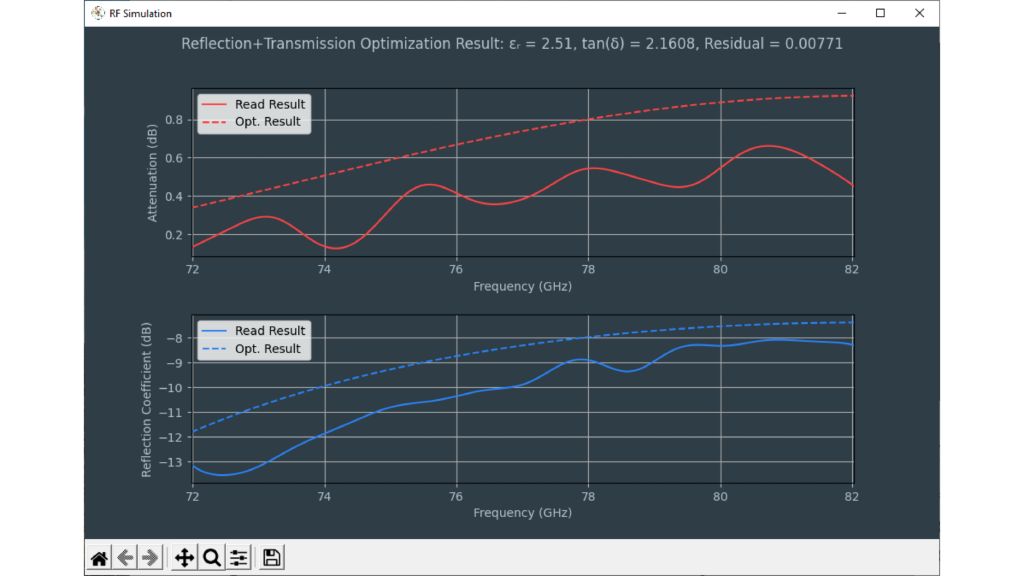
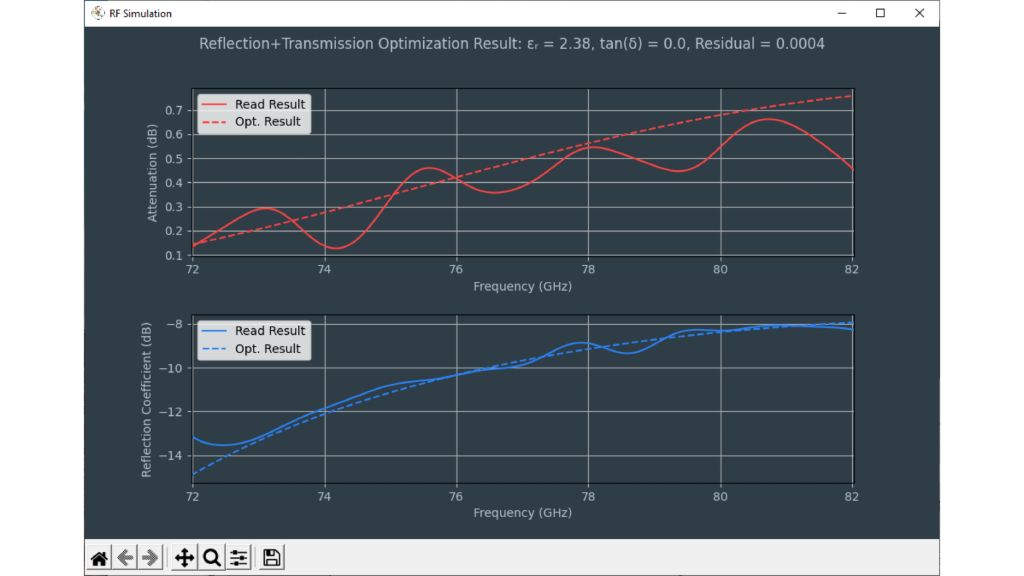
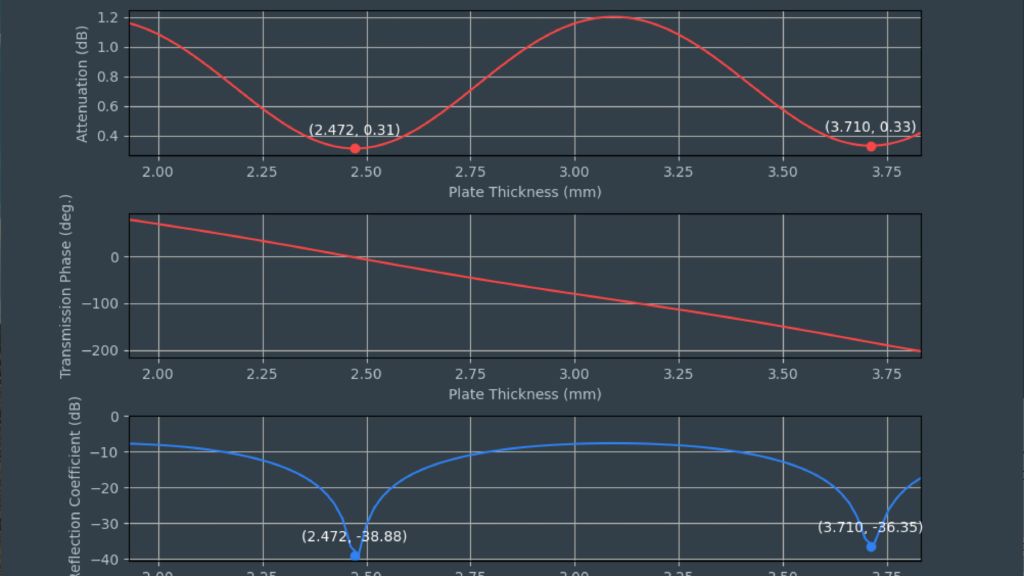
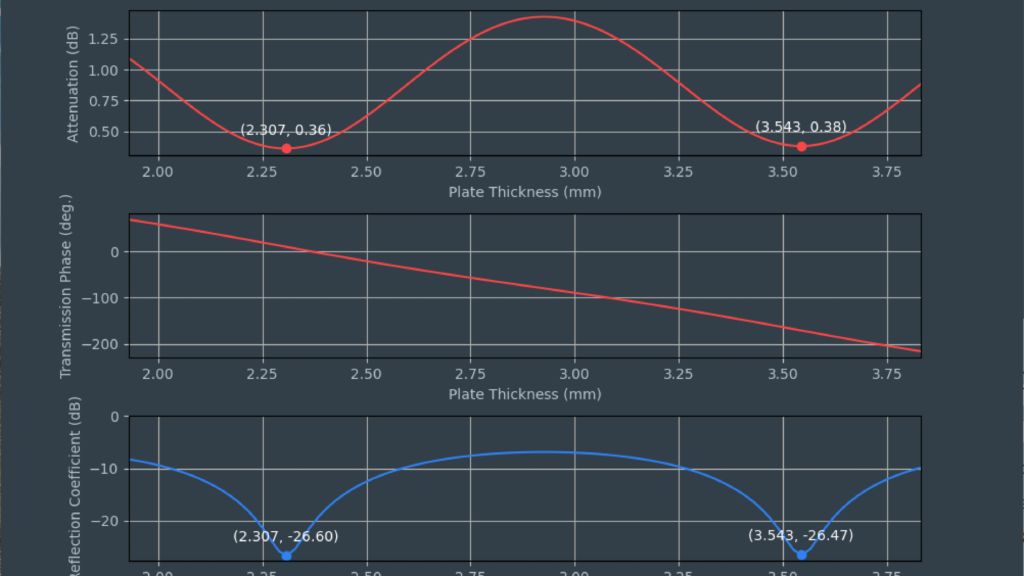
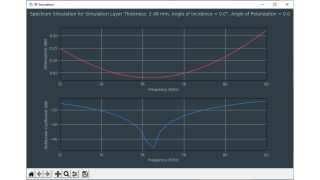
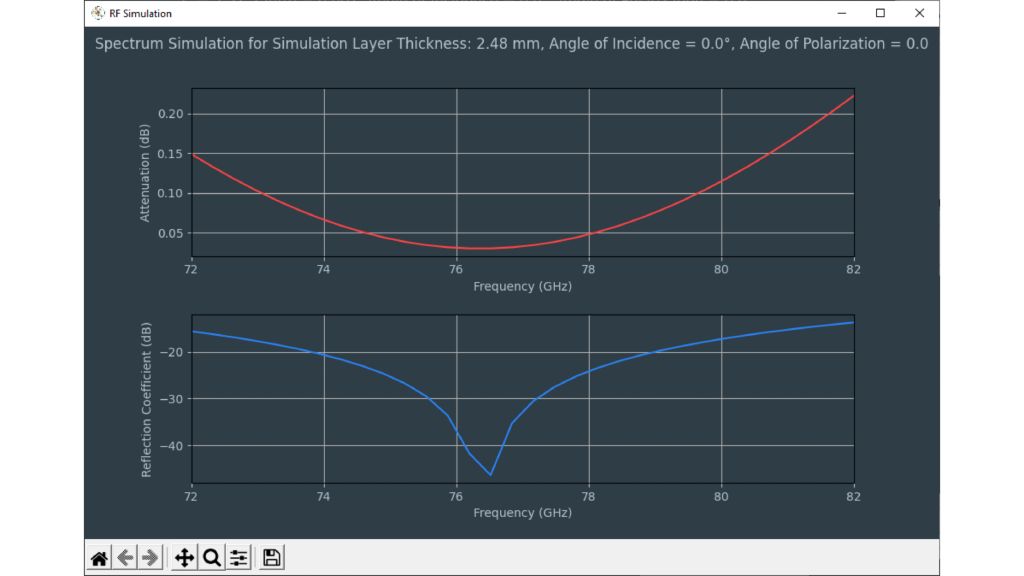
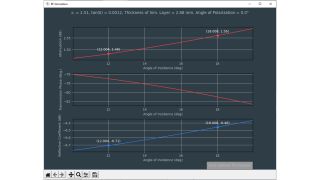
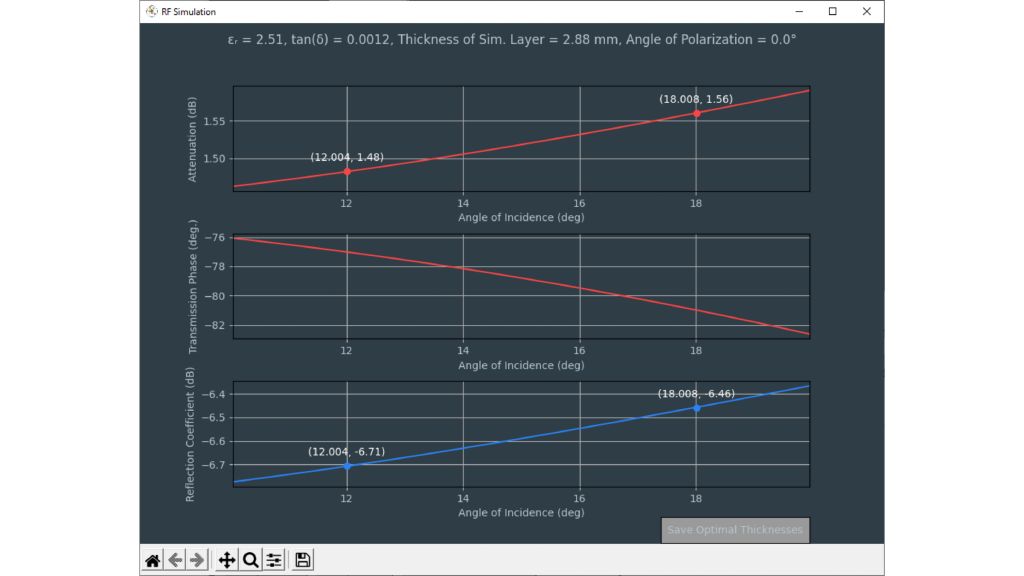
Los sensores radar ocultos en los parachoques de los automóviles deben transmitir en el dominio frecuencial correcto. Para lograr que los sensores queden bien camuflados, las áreas transparentes al radar suelen tener exactamente la misma pintura que el resto del vehículo. A la hora de seleccionar la pintura y el revestimiento de los parachoques es necesario conocer las propiedades del material. Antiguamente se utilizaban para ello configuraciones de medida cuasiópticas o basadas en guía de ondas con analizadores de redes vectoriales (VNA). La siguiente ficha de aplicación describe un método simplificado para la caracterización de materiales en el dominio frecuencial de los radares de automóviles (de 76 GHz a 81 GHz) con el comprobador de radomos R&S®QAR50 para automoción.